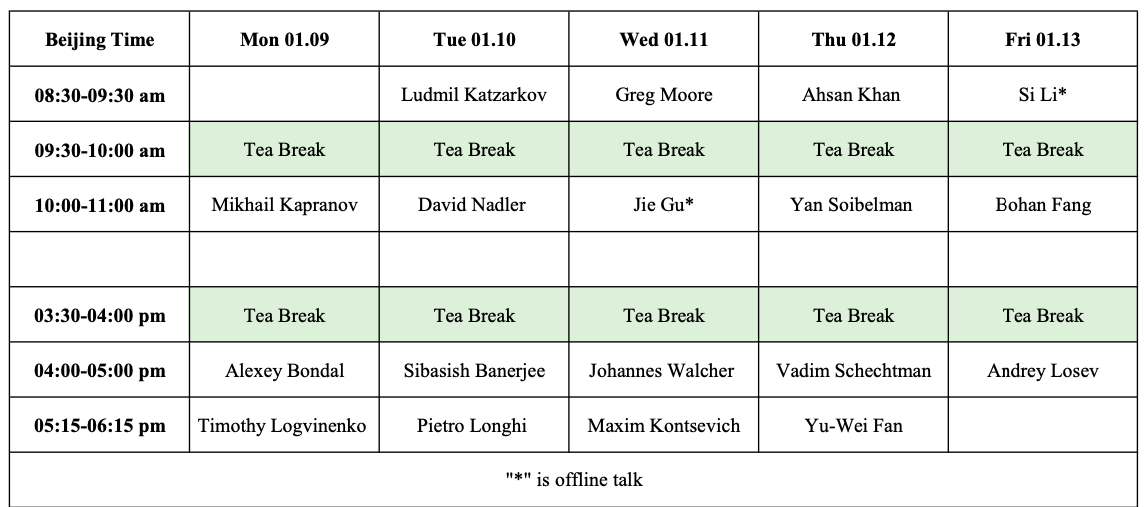
Table of Contents
Sanya: Infrared
Zoom Number: 271 534 5558 Password: YMSC
Jan 09
Timothy Logvinenko
Speaker: Timothy Logvinenko LogvinenkoT@cardiff.ac.uk
Title: Skein-triangulated representations of generalised braids
The braid group Br encodes configurations of n non-touching vertical strands (“braids”) up to continuous transformations. There are many examples where Brn acts on the derived category of an algebraic variety: the minimal resolutions of Kleinian singularities, the cotangent bundles of flag varieties, etc.
In this talk, I introduce a new structure: the category GBr of generalised braids. These are the braids whose strands are allowed to touch in a certain way. For triangulated categories, it is natural GBr . These relations generalise the famous skein relation used to define oriented link invariants to impose certain relations which result in the notion of a skein-triangulated representation of such as Jones polynomial.
We give two examples of skein-triangulated actions of GBr : on the cotangent bundles of varieties of full and partial flags in 𝐂𝐂n and on categorical nil-Hecke algebras. The latter example shows that any categorical action of Brn can be lifted to a skein-triangula