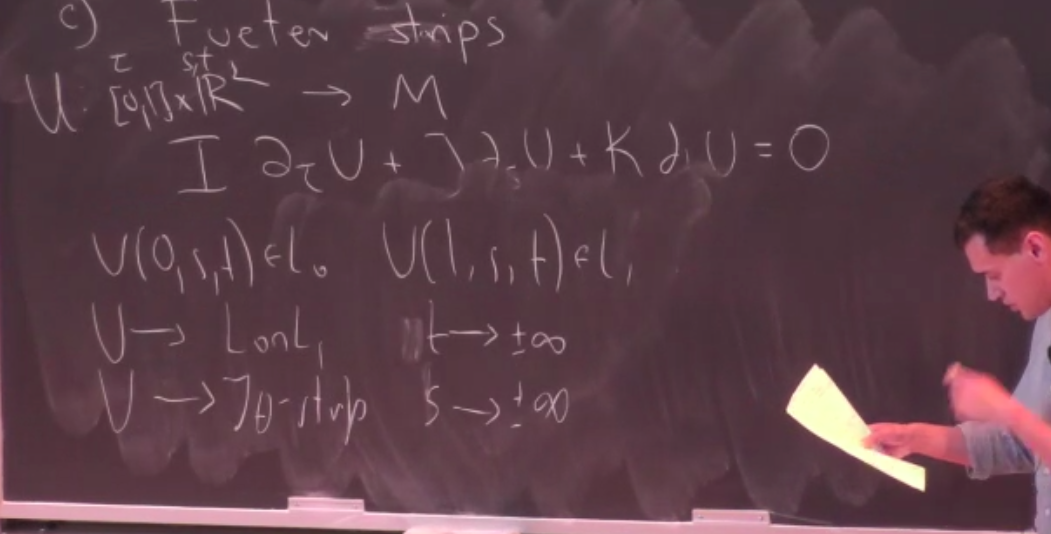This week we have the Gauge theory workshop in MSRI, one can participate online. I watched the one by Cherkis on AL? spaces and Doan on Fueter equation.

Cherkis and Kapustin constructed certain moduli spaces, in the late 90s. Recently, there are classifications on the math side about these spaces, one of the authors is also my friend Chen Gong, also advisor of my friend. These spaces are instanton or monopole moduli spaces with 4 real dimensions. There are some nice slices that will remind me the salient features. I wish I talked to him more during the summer when he visited UC Berkeley, but now is the next best time to ask him questions.

  

I didn't get the geometric picture why such morphism category is the Fukaya-Seidel category. Consider some hyperkahler space, two complex Lagrangians $L_1, L_2$ (BAA type, I-complex, $\omega_J, \omega_K$-Lagrangian). Say intersects transversely. Then, intuitively, from the point of view of $L_1$, the second Lagrangian is locally a graph $dW$, and then, the expected output is the Fukaya-Seidel category.

But, in general, the second Lagrangian is not a $dW$ type, how and why it works?

Why we have 3d mirror symmetry in this game?

How is this related to the Kontsevich-Soibelman-Kapranov story? Haydys story? Gaiotto-Neitze-Witten story?

I think Doan and Rezhichov are up the hill in person, so maybe one can ask them directly.